A handy guide to homophones, homonyms, and homographs

Suede and swayed. Mine and mine. They're homophones, right? No, wait — homonyms? Are homophone and homonym synonyms? And what's the deal with homographs, anyway? How do they fit in? At least you're not in fourth grade anymore, so you don't have to worry about it. Unless...

...you're a fourth-grade teacher! Or you have a son or daughter in fourth grade. In that case, you've come to the right place to straighten out your phones, nyms, and graphs of the homo variety once and for all.

For starters: Homophones are words that sound the same but have different spellings. Homographs are words that are spelled the same but have different pronunciations. Homonyms are words that sound the same and are spelled the same.

Subscribe to The Week

Escape your echo chamber. Get the facts behind the news, plus analysis from multiple perspectives.

SUBSCRIBE & SAVE

Sign up for The Week's Free Newsletters

From our morning news briefing to a weekly Good News Newsletter, get the best of The Week delivered directly to your inbox.

From our morning news briefing to a weekly Good News Newsletter, get the best of The Week delivered directly to your inbox.

Sign up

The relationship between the three can be represented in a Venn diagram, like this one:

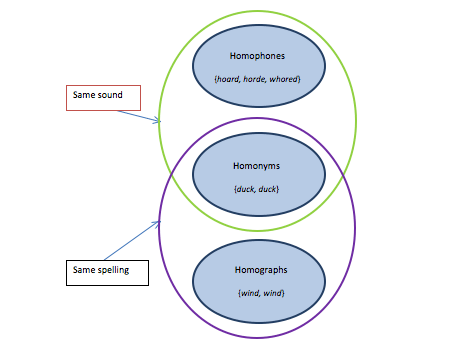
In fact, Venn diagrams are so much fun to make that you can find plenty of others on the internet that show the relationship between homophones, homonyms, and homographs. The trouble is, the well-meaning people who make these graphs get carried away, because Venn diagrams are the most fun when you can have not just two, but three intersecting circles. (More than three is just a mess.) To maximize the fun, these other diagrams make an elaborate, three-circle production out of the whole thing, with three pairwise intersections and one grand three-way intersection in the middle.

To fill that third circle, they end up bringing synonyms into the mix, which means that we're now talking about not just spellings and pronunciations, but meanings as well. That complicates the definitions of homophone, homonym, and homograph. Furthermore, they then have to populate all the intersections with sets of words that never used to have their own special name: words that are spelled more than one way (like fulfill and fulfil), and words that are pronounced more than one way (e.g. harass). And in what should be the most exciting set of all, the intersection of all three circles, what do we get? Words that sound the same, are spelled the same, and (get this) have the same meaning! In other words, pairs such as boat "a vehicle for traveling on water" and boat "a vehicle for traveling on water." Wow.

So two main circles and just one intersection is definitely the way to go for maximum clarity. However, there is one modification we could make to this diagram to make it even simpler. What if we were to do this?

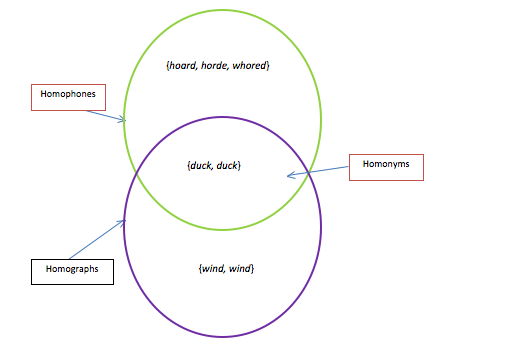
This is the diagram I like. It represents a simpler definition for homophone and homograph, too. Instead of defining homophones as "words that sound the same but have different spellings," we can just drop the second condition. Instead of defining homographs as "words that are spelled the same but have different pronunciations," we can just mention the spellings and leave it at that.

But can you handle a diagram like this one? Can you accept homonyms as kinds of homophones and kinds of homographs? Here's a test. If you can accept squares as a kind of rectangle, chili as a kind of soup, and senators as a kind of congressman or congresswoman, this is the diagram for you.